Contour Integration

A contour is a finite collection of paths joined end to end. A path can be represented as a continuous function form an closed iterval to \(\mathbb{C}\) as follows

\[ \gamma: [a~ b]\subset \mathbb{R} \to \mathbb{C}; \quad \gamma = \gamma(t)\]

Then the integration of any complex function along this path is is given by

\[\int_\gamma f(z)dz = \int_a^b f(t)~\gamma'(t)~dt = \sum_{i=1}^n f(t_i) \left[\gamma(t_i)-\gamma(t_{i-1})\right]\]

Question: Find the integration of \(f(z)=z^2\) along the parabolic path from \(0\) to \(1\).

Answer: In order to find the integration we have to find to parametrize the curve as \(\gamma(t)=t+t^2i\), \(t\in [0,1]\).

png

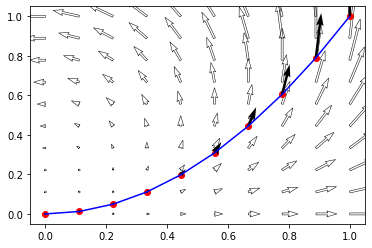
Numerical Computation¶

We can subdivide the curve into equal parts and then compute the sum as given in the definition. For 100 subdivisions we have the following result

\(\displaystyle -0.681868679980602 + 0.675438053988273 i\)

We can improve the accuracy by increasing the number of subdivisions, For example the same integration for 1000 subdivisions will be

\(\displaystyle -0.668168668668 + 0.66753436803537 i\)

We can plot the result for a number of points to see the convergence in complex plane as follows

png

1. Parametrization¶

Now we do the same computation using the parametrization of the curve, hence the value turns out to be exactly equalt to

\(\displaystyle -0.666666666666667 + 0.666666666666667 i\)

Last modified on: 2023-01-05 00:02:30